 |
| Zero sum games (Only 1 winner and 1 loser), are all games like this? |
In nature we witness organisms competing within their own species and with other species for commodities such as resources, territory and sexual partners. Genetic evolution has carved out very complicated strategies to which these organisms are programmed to play out in their competitions.
Let's look at an example. Southern elephant seals live in colonies and can live on land for a long period of time. In these colonies the males arrive first to decide dominance, territory and hence harems which would result in the dominant male copulating with lots of females, leaving the weaker seals with no guaranteed mate. We shall explore a 1 versus 1 scenario where a clear alpha male has not been established. Let's assume that each seal goes all out i.e. will give all that they've got to the death. This means that there will be one survivor and one dead seal. Whoever survives will most likely have to fight again, yet it is probably majorly injured and tired and will not do so well... it could die in the next fight. If the amount of males is about 10 (which it normally is) it would have to fight at max 9 more big males to own the harem. Imagine that there is one seal who has genes which encourage it to flee when things get too deadly. He will have lost the fight but he will not be dead, as time goes by more male seals die and the victors are injured and tired. This surely is a great opportunity for the 'flee when deadly' seal to attack... the victor is majorly injured and is weaker and does not pose a deadly threat to the 'flee when deadly' seal. So the 'flee when deadly' seal becomes victorious. In a population where 'go all out' seals are the majority and only 1 or 2 'flee when deadly' seals exist, we will see the flourishing of the 'flee when deadly' gene. This means the 'flee when deadly' will become a majority, yet say there comes a young big male who has the 'go all out' gene. He will encounter a lot of 'flee when deadly' seals and will no doubt become victorious and we see the oscillation continue on.
In nature, however, this oscillation of these two different 'simplistic one way strategy' seals does not exist. Each seal plays a mixed strategy which has become a stable one. We involve a new game called fronting, where before battling it out the seals roar and look big to try and scare the opponent away. This means that if my roar and look is bigger than yours you will predict that you will most likely lose and therefore if you flee now you will not get injured and you will not waste energy (the cost of fleeing during fronting is less than the cost of losing and then fleeing in battling). The bigger seal benefits from this game too as he can win without wasting energy which could be used in copulating or fighting bigger less wimpy males.
Also when an alpha male is challenged by another male, he has everything to lose... he has his harem of females and his territory to lose. The challenger has nothing to lose but his energy and life, he has everything to gain though. The alpha male is alpha because he is most probably the strongest, if they battle the alpha male will 'go all out' as the cost of losing is great and we see that the cost of losing for the alpha is higher than the challengers. We see that the challenger flees when things 'get too deadly', he will recover and get bigger and try again another day. Of course as the alpha gets older he gets weaker, there will be a challenger who will be better and bigger than him, when this battle comes the alpha will fight hard but he will not fight to the death.. there is no bigger cost than dying. He will simply flee and survive as much as he can.
So we see a stable strategy arise... if X is against Y and Y has a much bigger 'front' than X, X will flee unharmed. If B is against Y but B is not that intimidated by Y, B and Y battle... the winner will be victorious when either B or Y flee, if B > Y , Y will flee and B will win. If B is against F and F is an alpha male but B is not that intimidated by F then B and F battle. F will battle hard and B will battle hard, the amount of cost, c, F will have = Fc, for B = Bc... Fc > Bc and if things get too deadly B will flee. If things look extremely deadly for F, F will flee and B will become the victor. Most contests can be decided via fronting, if not then the battles normally follow the rules I have laid out. Note that this strategy is only stable over many confrontations (iterated game). Otherwise it would be stable to just go all out as you only have one confrontation ever (go all in).
Let's see a video of an Elephant seal harem bout: (Similar to F Vs. B where F is alpha, Fc>Bc and Br > Bd (risk of injury to B has reached or has surpassed being deadly and hence B flees).
This is quite a complicated game to simulate using pure mathematical rules, but it can be done. Complicated strategies arise in iterated games and in games where not all the players are equal i.e. some seals are bigger than others and 1 seal is an alpha one. Some of the males have also adopted other strategies to copulate without confrontation (as the prize of the life game is simply to impregnate females to spread genes in future populations). Some males try and mate with the females in the harem... this is risky as the alpha male is normally close by, but the probability of getting the prize may be higher in this strategy and the cost may even be the same or less than confrontation (injury or flee).
We now see the importance of the concept of evolutionary stable strategies (ESS). An evolutionary stable strategy is one played by the majority of the population and an organism playing this strategy will on average do better i.e. generate more offspring than any mutant strategy (played by a small minority). This means the strategy will still be the most played strategy hence it is a stable one. This concept was introduced in detail by John Maynard Smith and George R. Price in Evolution and the theory of games.
The formal definition:
Let us assume that the population is infinite (classical evolutionary game theory) and that there exists a fraction 1 - m of majority organisms(X-organisms) who play a strategy X and fraction m of minority organisms(Y-organisms) who play a strategy Y. Two organisms are chosen uniformly at random to contend with each other. The fitness function F (which basically means the game) decides the pay-offs of the organisms. Let F(X/Y) denote the pay off X- organism gets when contending Y-organism and let F(Y/X) be the pay-off Y gets when contending X. X is a stable strategy if the pay-off is always higher when playing X for all X is not equal to Y and for small m.
The probability of a majority organism facing another majority organism is 1 - m and the probability of facing a minority organism is m. We can therefore formulate the expected fitness of both organisms:
(1-m)F(X/X) + (m)F(X/Y) For a majority organism.
(1-m)F(Y/X) + (m)F(Y/Y) For a minority organism.
This leads to the definition of an ESS:
A strategy is an ESS for the 2 player, symmetric game given by a pay-off function F, if for every strategy X is not equal to Y, there exists and m_Y such that for all 0 < m < m_Y (which means a fraction of the population which plays Y and this fraction > the rest of the minority), (1-m)F(X/X) + (m)F(X/Y) > (1-m)F(Y/X) + (m)F(Y/Y).
This definition holds if and only if either of these two conditions are met:
(1) F(X/X) > F(Y/X) or (2) F(X/X) = F(Y/X) and F(X/Y) > F(Y/Y)
=> F(X/X) (is more than or equal to) F(Y/X). This means that X must be a best response to itself and thus for any ESS X, the strategy profile (X, X) must also be a Nash equilibrium.
The Nash equilibrium for non-cooperative games was first applied to economic theory and won John Forbes Nash of Princeton the Nobel prize in economics.
Basically it can be explained like this: the strategies of two Agents T and Y who are playing a 2 player non-cooperative game are in Nash equilibrium if and only if T is playing the best strategy for itself taking into account Y's strategy and Y is playing the best strategy for itself taking into account T's strategy.
In the film A Beautiful Mind we can see what it was like for Nash to figure out this equilibrium:
We consider one more example where the Nash equilibrium and ESS are equated in a biological context. Consider the Anodorhynchus hyacinthinus parrot, where grooming is part of their behavior.
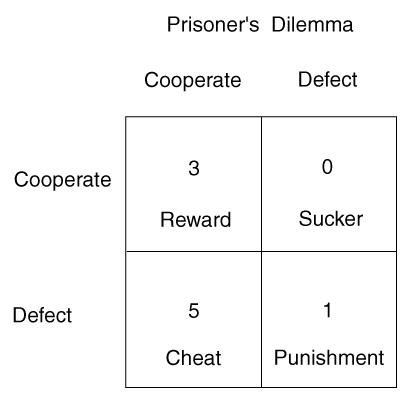
Their beaks cannot reach the tip of their head, so when they groom that part of their body is vulnerable to ticks. Ticks can be harmful to them as they carry disease, this disease could be fatal for the parrot. It would be in the parrots interest to have the ticks picked from its head but it needs to do this externally. This invokes the use of another parrot who can pick the ticks from its head. However we have just started a game as we can see mixed strategies arising. We could see parrots only receiving grooming and never returning the favor which would lead to it being groomed and not wasting energy in grooming others. We could see parrots only grooming others and not being groomed which would lead to energy loss and having ticks (fatal), these two strategies are normally called co-operate and defect. The game is an exact application of the prisoners dilemma:
The best strategy according to this pay-off matrix is to always defect i.e. to not groom. Always grooming leads to less 'pay-off' than always not grooming (still receiving from a groomer). This means that always not grooming is an ESS and is a Nash equilibrium. Taking in consideration to what the other person could do, you choose always not groom as this means your doing the best for yourself taking into account what the other person would do to better himself.
In the iterated version (over numerous times where the end of the iterations is not known) the always not groom is not an ESS. A tournament undertaken by Axelrode where programmers sent in there strategies to the iterated prisoners dilemma saw the Tit for Tat strategy to win, this strategy started out to 'always groom' but when being cheated on by a 'always not groom' or one which defected, the player would copy what happened to itself... so on the next go it will not groom.
This will be more of an accurate picture to our parrot grooming behavior as an ESS would have already evolved in that species.
Game theory has huge applications in Economics, Evolutionary biology, International politics and analysis of human behavior. It could also pave new advancement in robotic algorithms.


No comments:
Post a Comment